Weyl's lemma (Laplace equation)

In mathematics, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German mathematician Hermann Weyl.

1 Statement of the lemma
2 Heuristic of the proof
3 Generalization
4 "Weak" and "very weak" forms of the Laplace equation
5 References

Statement of the lemma

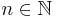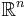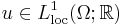Let $n \in \mathbb{N}$ and let $\Omega$ be an open subset of $\mathbb{R}^{n}$ . Let $\Delta$ denote the usual Laplace operator. Suppose that $u$ is locally integrable (i.e., $u \in L_{\mathrm{loc}}^{1} (\Omega; \mathbb{R})$ ) and that

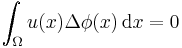
$\int_{\Omega} u(x) \Delta \phi (x) \, \mathrm{d} x = 0$ $\quad$ (Eq. 1)

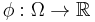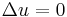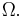
for every smooth function $\phi�: \Omega \to \mathbb{R}$ with compact support in $\Omega$ . Then, possibly after redefinition on a set of measure zero, $u$ is smooth and has $\Delta u = 0$ in $\Omega.$

Heuristic of the proof

Weyl's lemma can be proved by convolving the function $u$ with an appropriate mollifier, and then showing that the resulting function satisfies the mean value property, which is equivalent to being harmonic. The nature of the mollifer chosen means that, except on a set of measure zero, the function $u$ is equal to its own mollifier.

Generalization

Weyl's lemma follows from more general results concerning regularity properties of elliptic operators. For example, one way to see why the lemma holds is to note that elliptic operators do not shrink singular support and that $0$ has no singular support.

"Weak" and "very weak" forms of the Laplace equation

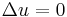The strong formulation of the Laplace equation is to seek functions $u$ with $\Delta u = 0$ in some domain of interest, $\Omega$ . The usual weak formulation is to seek weakly differentiable functions $u$ such that

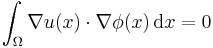
$\int_{\Omega} \nabla u (x) \cdot \nabla \phi (x) \, \mathrm{d} x = 0$ $\quad$ (Eq. 2)

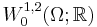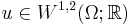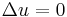for every $\phi$ in the Sobolev space $W_{0}^{1, 2} (\Omega; \mathbb{R})$ . A solution of (Eq. 2) will also satisfy (Eq. 1) above, and the converse holds if, in addition, $u \in W^{1, 2} (\Omega; \mathbb{R})$ . Consequently, one can view (Eq. 1) as a "very weak" form of the Laplace equation, and a solution of (Eq. 1) as a "very weak" solution of $\Delta u = 0$ .

References

Dacorogna, Bernard (2004). Introduction to the Calculus of Variations. London: Imperial College Press. ISBN 1-86094-508-2.
Gilbarg, David; Neil S. Trudinger (1988). Elliptic Partial Differential Equations of Second Order. Springer. ISBN 3-540-41160-7.
Stein, Elias (2005). Real Analysis: Measure Theory, Integration, and Hilbert Spaces. Princeton University Press. ISBN 0691113866.